• Article
• Accès libre
• Publié:03 juin 2024

Imagerie sans marquage à haute résolution et à grand champ de vision via une reconstruction de champ complexe à forme fermée et corrigée des aberrations

• Ruizhi Cao ,
• Cheng Shen et
• Changhuei Yang 

Nature Communications volume 15 , Numéro d'article :  4713 ( 2024 ) Citer cet article

• 2613 Accès

• 2 citations

• 96 Altmétrique

• Métriquedétails

Abstrait

Les méthodes d'imagerie computationnelle permettent aux microscopes modernes de produire des images haute résolution, à grand champ de vision et sans aberration. La microscopie ptychographique de Fourier peut augmenter le produit espace-bande passante de la microscopie conventionnelle, mais ses méthodes de reconstruction itérative sont sujettes à la sélection des paramètres et ont tendance à échouer en cas d'aberrations excessives. Les méthodes spatiales Kramers-Kronig peuvent reconstruire analytiquement des champs complexes, mais sont limitées par l'aberration ou par une amélioration de la résolution étendue. Nous présentons ici APIC, une méthode en forme fermée qui allie les points forts des deux méthodes tout en utilisant uniquement la correspondance NA et les mesures en fond noir. Nous établissons un cadre de récupération de phase analytique qui démontre la faisabilité de la reconstruction analytique du champ complexe associé aux mesures en fond noir. APIC peut récupérer des aberrations complexes d'un système d'imagerie sans matériel supplémentaire et évite les algorithmes itératifs, ne nécessitant aucune métrique de convergence conçue par l'homme tout en obtenant toujours une solution de champ complexe en forme fermée. Nous démontrons expérimentalement que l'APIC donne des résultats de reconstruction corrects là où la microscopie ptychographique de Fourier échoue lorsqu'elle est limitée au même nombre de mesures. L'APIC atteint un calcul 2,8 fois plus rapide en utilisant une taille de mosaïque d'image de 256 (dans le sens de la longueur), est robuste contre les aberrations par rapport à la microscopie ptychographique de Fourier et est capable de traiter les aberrations dont la différence de phase maximale dépasse 3,8π lors de l'utilisation d'un objectif NA 0,25 dans l'expérience.

Contenu similaire consulté par d'autres

Imagerie de phase quantitative variationnelle de Hilbert

Article Accès libre18 août 2020

Microscopie tridimensionnelle à fond clair avec résolution isotrope basée sur l'acquisition multi-vues et la reconstruction par fusion d'images

Article Accès libre29 juillet 2020

Repousser les limites de la microscopie optoacoustique grâce à la caractérisation de la réponse impulsionnelle totale

Article Accès libre09 juin 2020

Introduction

La recherche de techniques de microscopie capables de fournir simultanément une haute résolution et un grand champ de vision (FOV) peut améliorer la pathologie numérique et être largement appliquée dans d'autres applications d'imagerie à haut débit. L'imagerie computationnelle, pierre angulaire de la microscopie moderne, joue un rôle crucial dans la réalisation de ces objectifs. Au cours des dernières décennies, des progrès remarquables ont été réalisés dans les domaines de l'imagerie par fluorescence et sans marquage ^{1 , 2 , 3 , 4 , 5 , 6 , 7} . L'une de ces techniques représentatives sans marquage, la microscopie ptychographique de Fourier (FPM), exploite la puissance du calcul pour fournir des capacités de haute résolution et de correction des aberrations aux objectifs à faible ouverture numérique (NA) ^{1 , 2 , 8} . Le FPM fonctionne en collectant une série d'images à basse résolution sous un éclairage incliné et applique un algorithme de récupération de phase itératif de base pour reconstruire les caractéristiques de fréquence spatiale élevée et l'aberration optique de l'échantillon, ce qui permet d'obtenir une imagerie sans aberration à haute résolution qui préserve le champ de vision intrinsèquement large associé aux objectifs à faible ouverture numérique. Il augmente considérablement le produit de bande passante spatiale de la microscopie standard d'une manière simple mais étonnamment efficace. En raison de ces caractéristiques attrayantes, le FPM a trouvé diverses applications dans l'imagerie de phase quantitative, la métrologie des aberrations, la pathologie numérique et d'autres domaines ^2 , 9 .

Bien que le FPM soit une avancée importante dans la microscopie sans marquage, son algorithme de reconstruction itérative essentiel pose plusieurs défis. Tout d'abord, la reconstruction itérative du FPM est un processus d'optimisation non convexe, ce qui signifie qu'il n'est pas garanti qu'il converge vers la solution réelle ^{1 , 2 , 8 , 10 , 11 , 12 , 13} . En pratique, l'algorithme exécute des projections alternées entre l'espace réel et l'espace de fréquence spatiale jusqu'à ce que certaines conditions soient remplies, telles que le taux de diminution de sa fonction de perte atteigne une limite inférieure, l'exécution atteint le nombre d'itérations maximal autorisé ou l'algorithme satisfasse d'autres seuils métriques prédéfinis ^{1 , 2 , 10 , 11 , 12 , 13 , 14 , 15} . Par conséquent, le FPM ne garantit pas que la solution optimale globale soit jamais atteinte. Cela est problématique pour les applications exigeantes, telles que la pathologie numérique, où même de petites erreurs dans l'image ne sont pas tolérables. Français De plus, l'optimisation conjointe de l'aberration et du spectre d'échantillon peut échouer lorsque les aberrations du système sont suffisamment graves, ce qui conduit à des reconstructions médiocres ¹⁶ . La nature itérative de l'algorithme de reconstruction FPM a incité les chercheurs à adapter les concepts d'apprentissage automatique à sa mise en œuvre, dans le but de réduire la charge de calcul, de réduire les artefacts et de corriger les aberrations ^{17 , 18 , 19 , 20} . Ceux-ci, à leur tour, conduisent à d'autres problèmes, tels que la sensibilité contextuelle et une dérive potentiellement plus importante par rapport à la solution optimale globale. Il convient de se demander à ce stade s'il est possible de développer une solution sous forme fermée à cette classe de problèmes d'imagerie computationnelle, afin que tous ces défis puissent être relevés plus efficacement.

Français Des études récentes ont montré que le champ complexe peut être reconstruit de manière non itérative dans un scénario spécifique de microscopie à éclairage variable en faisant correspondre l'angle d'éclairage à l'angle d'acceptation maximal de l'objectif (l'angle de correspondance NA) et en exploitant l'analyticité du signal, par exemple, grâce à l'imagerie Kramers-Kronig dans le domaine spatial ^{21 , 22 , 23} . Ces résultats sont importants et percutants car ils éliminent le besoin d'un cadre de reconstruction itérative et ne nécessitent pas de critère de convergence conçu par l'homme. Cependant, il convient de noter que cette approche ne possède pas la capacité de corriger les aberrations hybrides ni d'offrir une grande amélioration de la résolution au-delà de la limite de diffraction de l'NA objectif. En tant que tel, le FPM reste un choix plus attrayant dans divers scénarios.

Dans cette étude, nous présentons une méthode analytique, appelée imagerie ptychographique angulaire avec méthode de forme fermée (APIC), qui allie les points forts des deux méthodes. L'APIC s'appuie sur la reconstruction de champs complexes à l'aide des relations Kramers-Kronig et utilise des techniques analytiques pour récupérer les aberrations et reconstruire le spectre de fréquence spatiale élevée associé au fond noir. En utilisant la correspondance NA et les mesures en fond noir, l'APIC est capable de récupérer des champs complexes à haute résolution et sans aberration lorsqu'un objectif à faible grossissement et à grand champ de vision est utilisé pour l'acquisition de données. À partir de simulations et d'expériences, l'APIC démontre une robustesse sans précédent contre les aberrations, tandis que le FPM échoue radicalement. En raison de sa nature analytique, l'APIC est intrinsèquement insensible aux paramètres d'optimisation et offre une solution de champ complexe analytique garantie. Nous montrons en outre que l'APIC fonctionne mieux que le FPM lorsqu'il est soumis à la même contrainte sur la taille des données d'entrée, car il ne nécessite pas une redondance de données trop importante nécessaire au FPM pour une bonne convergence. En intégrant des mesures en champ sombre, l'APIC atteint effectivement la même amélioration de résolution théorique que le FPM. Nous pensons que l'APIC représente une avancée décisive dans le domaine de l'imagerie computationnelle.

Résultats

Principe

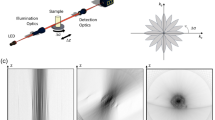
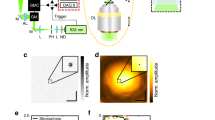
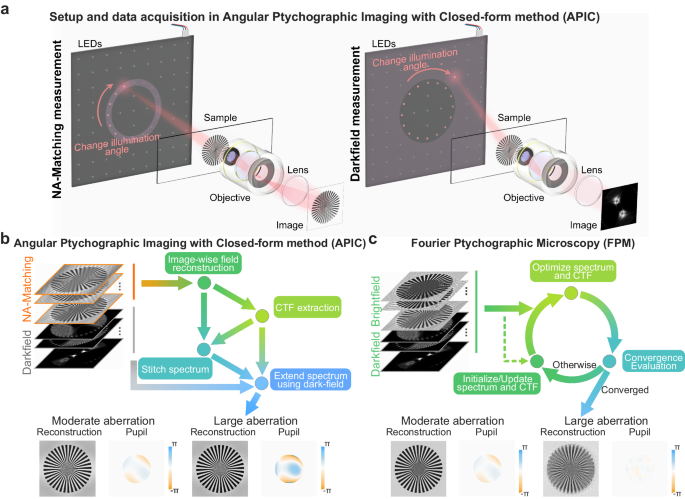
L'APIC collecte à la fois des mesures d'intensité de correspondance NA et de fond noir pour une reconstruction à haute résolution. Son processus de reconstruction commence par une résolution analytique du spectre de fréquence spatiale et de l'aberration de l'échantillon avec les mesures de correspondance NA. Ensuite, les mesures de fond noir sont utilisées pour étendre le spectre de fréquence spatiale de l'échantillon afin d'améliorer considérablement la résolution d'un système d'imagerie limité par NA. La configuration du système, le processus d'acquisition de données et son organigramme de reconstruction sont illustrés dans la Fig.  1. Dans l'étape d'acquisition de données de l'APIC, les LED dont les angles d'éclairage correspondent à l'angle d'acceptation maximal du système d'imagerie sont allumées séquentiellement. Les mesures sous ces éclairages d'angle de correspondance NA constituent les mesures de correspondance NA de l'APIC. Les LED dont les angles d'éclairage sont supérieurs à l'angle d'acceptation sont ensuite allumées successivement pour acquérir des mesures de fond noir. Dans les sections suivantes, nous utilisons le mot « spectre » comme abréviation pour le spectre de fréquence spatiale (la transformée de Fourier du champ complexe de l'échantillon). Nous notons que le spectre est différent de la transformée de Fourier d'une image acquise, qui est la transformée de Fourier d'une mesure d'intensité pure.

 

L'APIC fonctionne en reconstruisant d'abord le champ complexe correspondant aux mesures de correspondance NA en utilisant les relations Kramers-Kronig. Ces mesures sont prises avec des angles d'éclairage LED qui correspondent à l'angle de réception maximal de l'objectif. Pour un système d'imagerie réaliste, les aberrations se superposent inévitablement à la phase des spectres. Pour extraire les aberrations de l'objectif, nous nous concentrons sur la région de chevauchement dans leurs spectres (le chevauchement de deux CTF translatés, où la translation est indiquée sur le côté gauche de la Fig.  2 ). Comme les phases dépendantes de l'échantillon sont identiques dans la région de chevauchement des deux spectres, la soustraction de leurs phases annule le terme de phase dépendant de l'échantillon, ne laissant que les différences de phase entre les différentes parties de la fonction pupillaire (voir la Fig.  S16 pour plus d'informations). Par conséquent, les régions de chevauchement nous donnent une équation linéaire par rapport au terme d'aberration. En résolvant cette équation linéaire, l'aberration du système d'imagerie peut être extraite, qui peut ensuite, à son tour, être utilisée pour corriger les spectres reconstruits d'origine. Les spectres corrigés sont ensuite assemblés pour obtenir une image d'échantillon sans aberration et à résolution améliorée deux fois.

Nous pouvons ensuite étendre le spectre en utilisant les mesures en champ sombre. Dans cette étape, le spectre de reconstruction et l'aberration obtenus dans la première étape servent de connaissance a priori. La reconstruction étape par étape fonctionne de la manière suivante. Nous choisissons une mesure dont le spectre est le plus proche du spectre connu (par exemple, la i -ème mesure) et recadrons le spectre connu en fonction de ce qui est échantillonné dans cette mesure, comme le montre la figure  2. Ce spectre recadré ne contient cependant qu'une partie de l'information de la i -ème mesure. Notre objectif est de récupérer la partie inconnue du spectre afin qu'elle puisse être complétée pour l'extension du spectre.

Nous pouvons voir que la transformée de Fourier de notre i- ème mesure d'intensité consiste en une corrélation croisée des spectres connus et inconnus et de leurs autocorrélations. Dans ce qui suit, nous montrons qu'en utilisant le spectre connu, nous pouvons construire une équation linéaire par rapport au spectre inconnu, qui peut être résolue analytiquement.

Tout d'abord, l'autocorrélation de la partie connue est calculée et soustraite de la transformée de Fourier de la mesure. Après soustraction, l'autocorrélation de la partie inconnue et les corrélations croisées sont conservées. Une observation importante est que ces parties ne coïncident pas complètement dans le domaine de fréquence spatiale (Fig.  2 ). Ainsi, nous pouvons nous concentrer sur la région de non-chevauchement où la corrélation croisée contribue uniquement au signal.

Nous pouvons alors construire une équation linéaire par rapport au spectre inconnu. Lors du calcul de la corrélation croisée, l'un des signaux est décalé et multiplié par un autre signal. Le coefficient de corrélation est la somme de ce produit. En supposant que l'un des deux signaux est connu, nous utilisons essentiellement le signal connu comme pondération et calculons la somme d'une version pondérée de l'autre signal pour trouver ce coefficient. Il s'agit d'une opération linéaire. Ainsi, en appliquant le spectre connu, nous pouvons construire un opérateur linéaire qui prend le spectre inconnu et produit cette corrélation croisée. En extrayant la partie non chevauchante du terme de corrélation croisée, nous pouvons former et résoudre analytiquement une équation linéaire par rapport au spectre inconnu. C'est-à-dire que nous obtenons la solution sous forme fermée du spectre inconnu en résolvant cette équation.

Pour un système d'imagerie pratique, nous devons prendre en compte son aberration dans le processus d'imagerie. Pour correspondre à la mesure, l'aberration récupérée est initialement introduite dans le spectre connu recadré. Après avoir récupéré le spectre inconnu, l'aberration est corrigée et ce spectre corrigé est réintégré dans le spectre reconstruit. Ce processus s'arrête lorsque toutes les mesures en champ noir ont été reconstruites. La dérivation détaillée des méthodes de reconstruction de champ complexe analytique et d'extraction d'aberration susmentionnées se trouve dans la section 12 de la note supplémentaire.

Une fois les étapes ci-dessus terminées, nous obtenons une image d'échantillon à haute résolution et sans aberration. La résolution optique théorique de l'APIC est déterminée par la somme de l'NA d'éclairage et de l'NA objectif, ce qui est identique aux formules de résolution NA du FPM ¹ . Nous notons que le FPM nécessite un processus itératif pour récupérer le spectre et est sensible au choix des paramètres d'optimisation. En revanche, l'APIC récupère analytiquement le spectre réel. Cette approche directe et efficace distingue l'APIC du FPM, offrant un processus de récupération de spectre plus simple et plus robuste. Dans la section suivante, nous rendrons compte de notre démonstration expérimentale selon laquelle l'APIC est efficace sur le plan informatique et permet des reconstructions de champs complexes cohérentes et de haute qualité même sous de grandes aberrations, tandis que le FPM a du mal en raison de la complexité accrue de son problème d'optimisation.

Résultats de l'expérience

Nous avons utilisé un objectif à faible grossissement (grossissement 10×, NA 0,25, Olympus) pour l'acquisition des données. Un anneau LED (anneau Neopixel 16, Adafruit) collé sur un réseau LED (matrice LED RGB 32 × 32, Adafruit) a servi d'unité d'éclairage. Les deux groupes de LED ont été montés sur une platine motorisée pour le réglage de la position et de la hauteur, et ils ont été contrôlés individuellement par deux cartes Arduino (Arduino Uno, Arduino). Au cours du processus d'acquisition, nous avons allumé une LED à la fois et déclenché simultanément la caméra (Prosilica GT6400, Allied Vision) pour capturer une image lorsque la LED était allumée. Ce processus s'est poursuivi jusqu'à ce que toutes les LED souhaitées soient allumées une fois. Nous avons ensuite effectué la reconstruction en utilisant à la fois APIC et FPM. L'étalonnage du système se trouve dans la section 1 de la note supplémentaire.

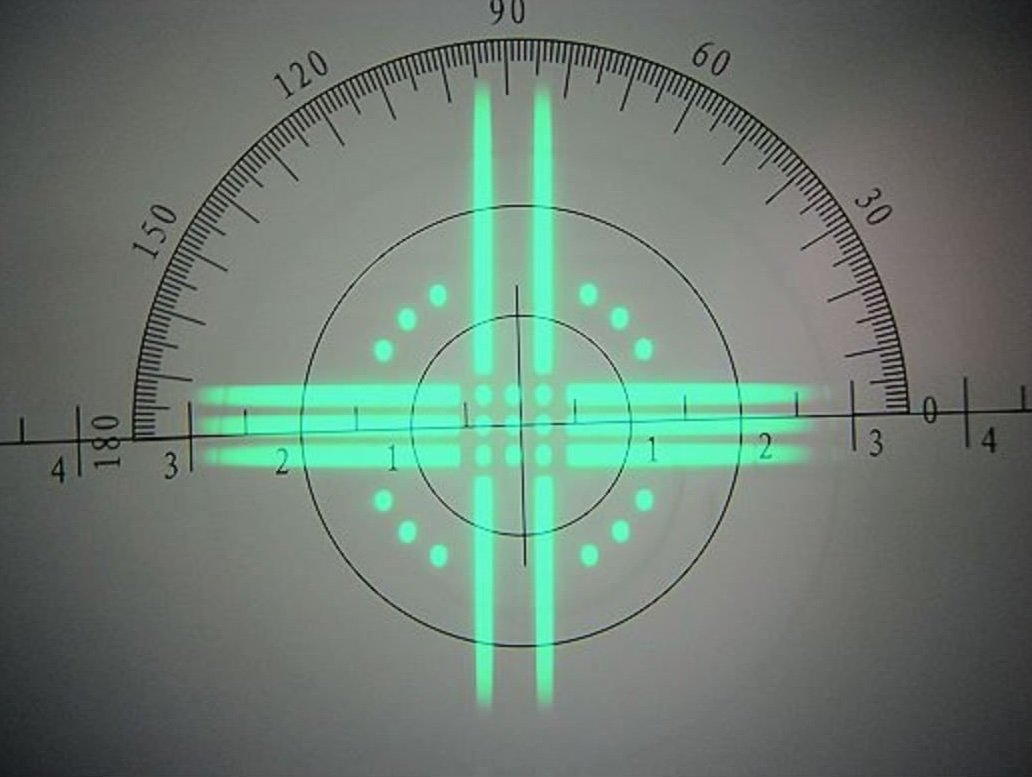
Français Dans notre première expérience, nous avons imagé une cible en étoile Siemens et avons choisi d'acquérir un petit ensemble de données pour effectuer une reconstruction à l'aide d'APIC et de FPM. L'ensemble de données acquis dans cette expérience comprenait 9 mesures en champ clair, 8 mesures de correspondance NA et 28 mesures en champ noir. Nous notons qu'il existe des travaux qui appliquent un schéma d'éclairage multiplexé pour réduire le nombre de mesures en FPM ^11 , 12 , ces méthodes ne sont pas aussi fiables que le schéma d'acquisition de données FPM conventionnel. Ainsi, nous nous concentrons uniquement sur le schéma d'acquisition le plus fiable dans cette étude. Le taux de chevauchement nominal des pupilles de balayage était d'environ 65 %. Dans nos expériences, l'algorithme de reconstruction FPM de Gauss-Newton du second ordre a été appliqué pour la reconstruction car il s'est avéré être l'algorithme de reconstruction FPM le plus robuste ¹³ , et la somme de toutes les mesures a été utilisée pour l'initialisation. Nous notons également que nous avons utilisé 6 ensembles de paramètres dans la reconstruction du FPM et avons choisi le meilleur résultat, car la qualité de reconstruction du FPM dépend fortement de ses paramètres. Certains résultats FPM représentatifs sont également présentés dans la Fig.  3 , ce qui confirme cette dépendance des paramètres. Au contraire, la fidélité et l'exactitude sont garanties dans APIC, bénéficiant de son cadre de récupération de phase analytique. Nous avons constaté qu'APIC était capable de restituer le champ complexe correct alors que FPM échouait, comme le montre la Fig.  3. Comme le montre le résultat, les rayons plus fins reconstruits étaient déformés dans tous les résultats de reconstruction de FPM. De plus, des artefacts de reconstruction ondulés notables existaient dans les phases reconstruites par FPM. Lorsque les mesures ont été transmises à APIC, les phases et les amplitudes reconstruites étaient moins ondulées. L'amplitude reconstruite est également plus proche de la vérité fondamentale, qui est échantillonnée à l'aide d'un objectif à NA élevé. Nous soulignons que lorsque la vérité fondamentale n'est pas donnée, les trois résultats FPM présentés dans la Fig.  3 peuvent être perçus comme une bonne reconstruction dans la pratique car ils préservent un bon contraste et sont riches en détails. Cependant, ces reconstructions sont de faible fidélité car elles s'écartent toutes de la vérité fondamentale que nous avons acquise. Nous pouvons constater que certains rayons de la cible en étoile de Siemens manquaient dans la reconstruction du FPM, ce qui indique l'échec du FPM. Cette expérience a démontré la capacité d'APIC à mieux récupérer un champ complexe à haute résolution lorsque la taille des données brutes est limitée, car il s'agit d'une méthode analytique et elle ne repose pas autant sur la redondance de chevauchement des pupilles pour la convergence des solutions que le FPM exige.

Il convient également de noter que pour une mosaïque d'image d'entrée d'une longueur de 256 pixels des deux côtés, la reconstruction APIC a pris 9 secondes sur un ordinateur personnel (CPU : Intel Core i9-10940X avec 64 Go de RAM), tandis que FPM a nécessité 25 secondes pour terminer la reconstruction. L'efficacité de calcul relative d'APIC peut encore être attribuée à la nature analytique de son approche par rapport à FPM. Nous notons que cette efficacité de calcul dépend de la taille de la mosaïque d'image : plus la mosaïque est petite, plus APIC peut être efficace (voir la section 6 de la note complémentaire pour plus d'informations). Comme il est généralement préférable de diviser une grande image en mosaïques plus petites dans le calcul parallèle, l'efficacité de calcul d'APIC pour les mosaïques plus petites correspond bien aux considérations de calcul pratiques.

Français Dans l'expérience suivante, nous avons étudié la robustesse de l'APIC et du FPM pour traiter les aberrations optiques. Pour cette expérience, nous avons acquis un total de 316 images, qui consistaient en 52 mesures normales en champ clair, 16 mesures de correspondance NA et 248 mesures en champ noir. Le taux de chevauchement nominal de la pupille de balayage de notre ensemble de données était d'environ 87 %, et le NA synthétique théorique final était égal à 0,75 lorsque toutes les mesures en champ noir ont été utilisées. Nous notons que ce degré élevé de chevauchement du spectre a été choisi pour fournir une redondance de données suffisante pour les meilleures performances du FPM. L'APIC ne nécessite pas un ensemble de données aussi volumineux (des exemples peuvent être trouvés dans la Fig.  3 et la Fig.  S3 de notre note supplémentaire). Dans notre reconstruction, l'APIC n'a utilisé que les mesures de correspondance NA et de champ noir, tandis que le FPM a utilisé l'ensemble de données, y compris ces 52 mesures en champ clair supplémentaires correspondant à des angles d'éclairage inférieurs à l'angle d'acceptation de l'objectif.

Nous avons délibérément défocalisé une cible en étoile Siemens pour évaluer les performances des deux méthodes sous différents niveaux d'aberration. Dans cette expérience, l'échantillon a été défocalisé à différents niveaux et les informations de défocalisation ont été masquées aux deux méthodes. Les résultats de FPM et APIC sont présentés dans la Fig.  4a . De toute évidence, pour les grandes aberrations dont l'écart type de phase dépassait 1,1π (le cas où la cible en étoile Siemens était défocalisée de 32 µm et la différence de phase maximale est d'environ 3,8π), FPM n'a pas réussi à trouver la bonne solution et les images reconstruites étaient considérablement différentes de la vérité fondamentale, même lorsque l'algorithme indiquait que son critère de convergence était atteint. À un niveau d'aberration inférieur, les reconstructions d'amplitude de FPM semblaient proches du cas idéal. Cependant, les phases reconstruites étaient sensiblement différentes du résultat lorsqu'aucune défocalisation n'était introduite. En revanche, APIC était très robuste à différents niveaux d'aberrations. Bien que le contraste de la reconstruction de l'APIC ait diminué sous l'effet d'aberrations plus importantes, il a récupéré les aberrations correctes et a donné des reconstructions de champ complexes à haute résolution qui correspondaient au résultat de mise au point. La résolution mesurée pour FPM et APIC est d'environ 870 nm lorsque les mesures de mise au point ont été utilisées, ce qui est proche de la résolution théorique de 840 nm (Fig.  S4 ).

Pour tester les deux méthodes sous des aberrations plus complexes, nous avons utilisé un objectif Olympus obsolète (grossissement 10×, NA 0,25) conçu pour fonctionner avec un autre type de lentille tubulaire pour la mesure d'image dans cette expérience particulière. Un échantillon de cellules d'adénocarcinome thyroïdien humain a été imagé pour voir leurs performances. Comme l'écart type de la phase de l'aberration du système d'imagerie était proche de 2π/5, le FPM n'a pas réussi à reconstruire une image haute résolution. D'après la Fig.  4b , l'amplitude reconstruite du FPM était fortement déformée par les artefacts de reconstruction. L'APIC a récupéré tous les détails les plus fins qui correspondaient bien à l'image que nous avons acquise en utilisant un objectif NA 0,75.

Nous avons ensuite mené une expérience en utilisant un échantillon de cellules cancéreuses du sein colorées à l'hématoxyline et à l'éosine (H&E). Nous avons utilisé des LED rouges, vertes et bleues pour acquérir des ensembles de données pour ces trois canaux différents, puis nous avons appliqué l'APIC pour la reconstruction. Dans cette expérience, l'échantillon a été placé à une hauteur fixe dans le processus d'acquisition des données. En conséquence, nous observons différents niveaux de défocalisation dans différents canaux se trouvant au-dessus des aberrations chromatiques de l'objectif (Fig.  S5 ). Pour acquérir l'image de vérité terrain, nous sommes passés à un objectif 40× et avons focalisé manuellement chaque canal. Nous avons calibré les angles d'éclairage pour le patch central (longueur de côté : 512 pixels) puis calculé les angles pour les patchs hors axe à l'aide de la géométrie. Ces angles d'éclairage calibrés ont été utilisés comme paramètre d'entrée dans notre reconstruction. La région reconstruite finale est un carré de longueur de côté de 1,2 mm dans cette expérience.

L'image couleur reconstruite est présentée dans la Fig.  5. La comparaison des trois canaux est présentée dans notre note supplémentaire (Fig.  S5 ). À partir des images agrandies de la Fig.  5 , nous pouvons voir que les reconstructions de FPM étaient bruyantes pour le canal bleu. Nous avons constaté que FPM ne fonctionnait pas bien avec cet échantillon faiblement absorbant sous un niveau d'aberration relativement élevé. Il n'a pas réussi à extraire l'aberration du système d'imagerie. En tant que telle, l'image couleur générée par FPM est apparue granuleuse et les informations de haute fréquence spatiale n'ont été que partiellement récupérées. Nous voyons également que la reconstruction couleur d'APIC a conservé toutes les caractéristiques de haute fréquence spatiale qui correspondaient étroitement à la vérité de base que nous avons acquise. Cela démontre que la reconstruction des aberrations et du champ complexe d'APIC est considérablement plus précise que celle de FPM.